股票杠杆软件有哪些

倪世杨 Z0019629

历史波动率锥是判断当前隐含波动率高低的重要工具，在波动率交易里有重要意义。常见计算方法为采用滚动的、重合的窗口计算HV，再取结果分布的分位数。这一方法尽管直观，却人为在HV中引入了自相关性：比如计算HV30，第30个交易日的HV和第31个交易日的贡献了29天的数据，很难有较大差异。这意味着由此计算而得的历史波动率锥会低估波动率的样本分布离散程度。

Hodges 2002对此有研究。文章发现在收益IID、波动率不变的假设下，重合窗口采样下实际波动的样本离散程度是非重合窗口下的

    

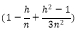
。笔者在《重合窗口采样下，实现波动样本方差调整系数的推导过程》(下简称《推导过程》，请联系笔者索要相关链接)一文中详述了这一结果的推导过程。本文将这一结果运用于实践，量化这一系数对波动率锥的影响程度，并结合当下行情判断商品市场上哪些期权偏贵。

怎样将修正系数表达成HV分布被压缩程度

我们首先理清修正系数怎么用到历史波动率锥的计算上。

严谨地说，Hodges 2002证明了在收益IID的情况下，

    

当中T为样本中的log收益率个数，h为历史波动率计算窗口，

    

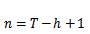
为HV的样本个数。一段时间的实际波动为样本log收益率的平方和，一组数据的样本离散程度类似该组数据的样本方差。具体定义在XX日发文中有详述。

构建历史波动率锥时我们关注HV的历史分位数。由于调整量纲的操作并不影响数据大小排序，某个分位数的HV应该等于该分位数的实现波动开根号再年化。所以我们只需取得实现波动的分布即可。

Hodges 2002的结果说明重合窗口采样会让实现波动的样本方差大致缩小为原来的

    

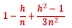
(确切得说，是在可重复试验的假设下，重合窗口采样会让实现波动的样本方差的大样本均值缩小为原来的

    

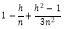
。现实里每次实验重合窗口采样对样本方差的影响都是随机的，用一个数字来描述，实在是不得已而为之的方法)。这意味着重合采样下，实现波动的样本标准差会缩小为非重合窗口的

    

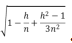
。对于每一个实现波动的值，我们可以先计算其离样本均值的偏离程度，在除以这一系数，再加上样本均值，就能得到修正后的实现波动。

修正系数有多大

如前所述，当表达成“重合窗口采样会将HV分布压缩多少倍时”，修正系数可以写成

    

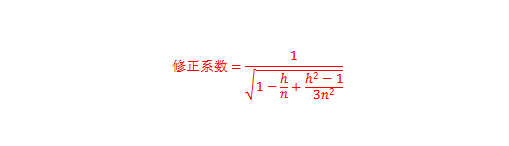
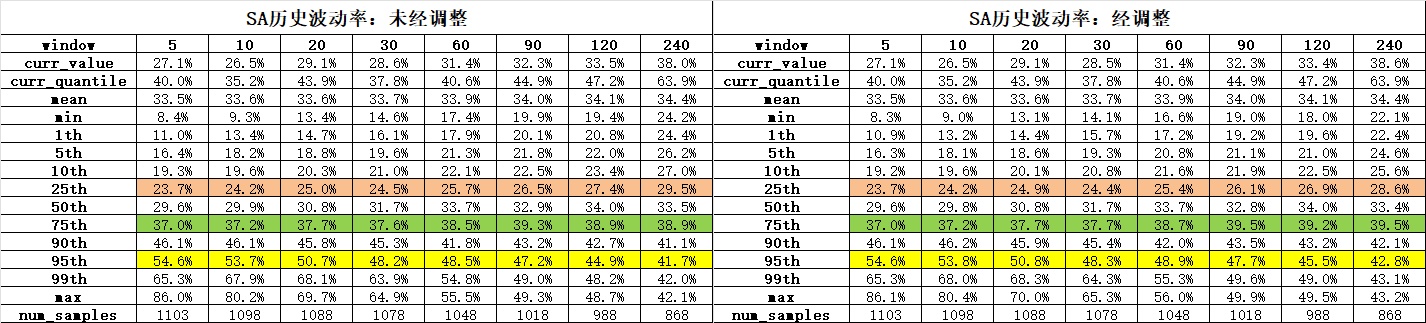
修正系数有多大？修正系数受到HV计算窗口和样本量影响。显然窗口越大、样本量越小，修正系数越大；但实操中为确保历史波动率锥有代表性，不会将样本量设置得太小。这里我们将数据起点设置为2020年1月1日，看看每个品种HV的修正系数有多大。

    

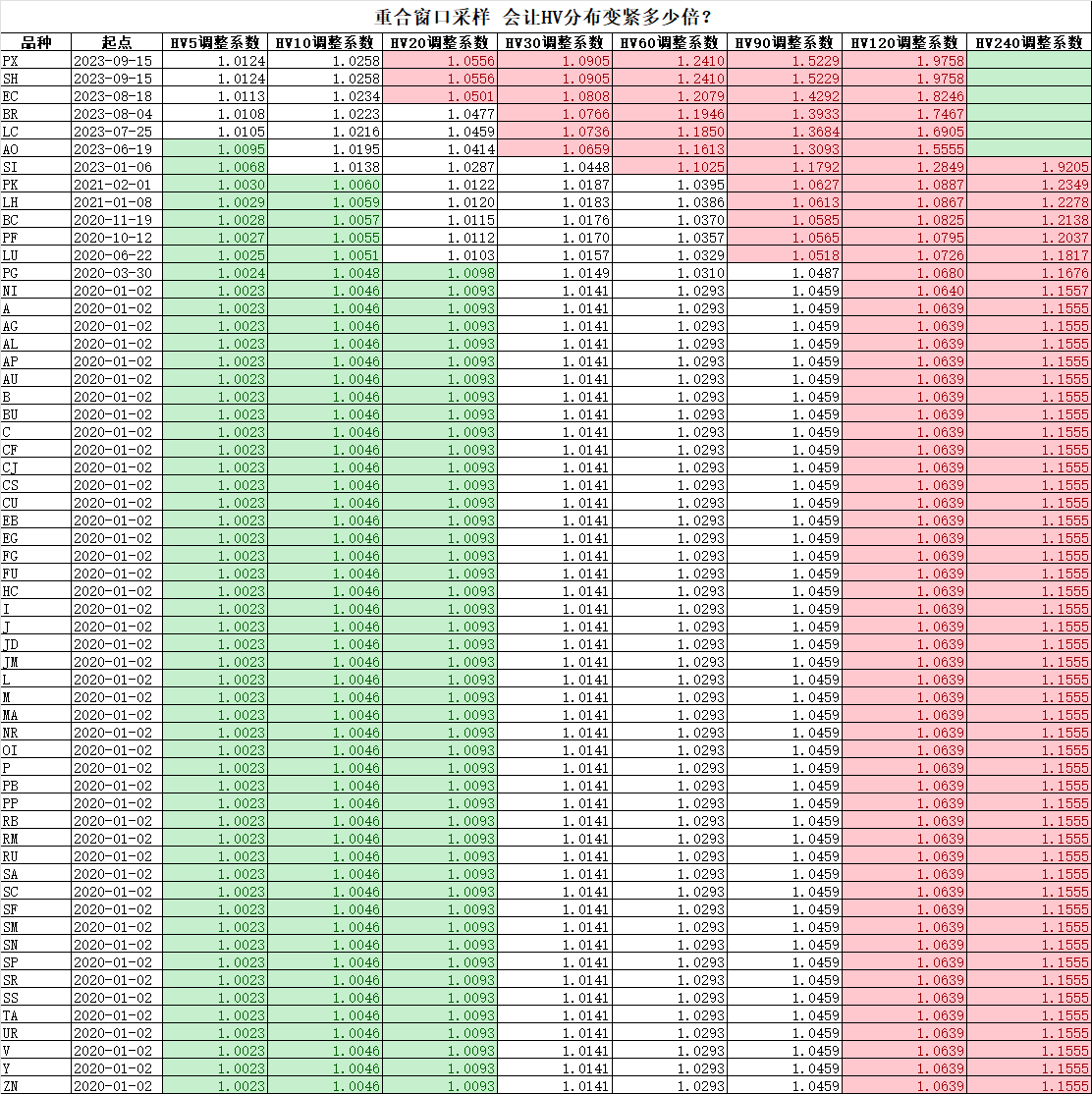
结果总结如下：

1. 对5日、10日HV，不做调整亦可。重合窗口采样对大部分品种波动率分布的扭曲程度有限，大部分在1%以下。

2. 对20、30日HV，要关注在23年下年后上市的品种。计算20日HV时，重合窗口采样对上市较晚的PX、SH、EC历史波动率分布的压缩程度在5%左右，这在EC上可能较明显。计算30日HV时，23年年中之后上市的品种均有5%以上的扭曲。

3. 对半年以上的HV，大部分品种都要注意重合窗口造成的波动率分布被压缩的问题。标注可以看出，HV120和HV240大部分调整系数都在1.05以上。

我们再来看两个具体的品种。对上市时间较短的EC，小样本使得各个大窗口HV的估计都比实际更紧。注意到各个窗口下EC波动率的均值显著高于其中位数，这意味着EC波动率显著右偏，即高波动的波动偏离均值很大，而低的波动相对没那么大，这和实际体验显然相符。这种情况下“HV分布被压缩”意味着EC未调整过的HV低分位数高估了低波状态下的实际波动水平 。根据测算，EC HV30 的25分位数应在47.7%左右，比简单测算低了3个vol；而HV90的25分位数应在58.4%左右，比简单测算低了10个vol。这点或许对场外交易台有参考价值。

    

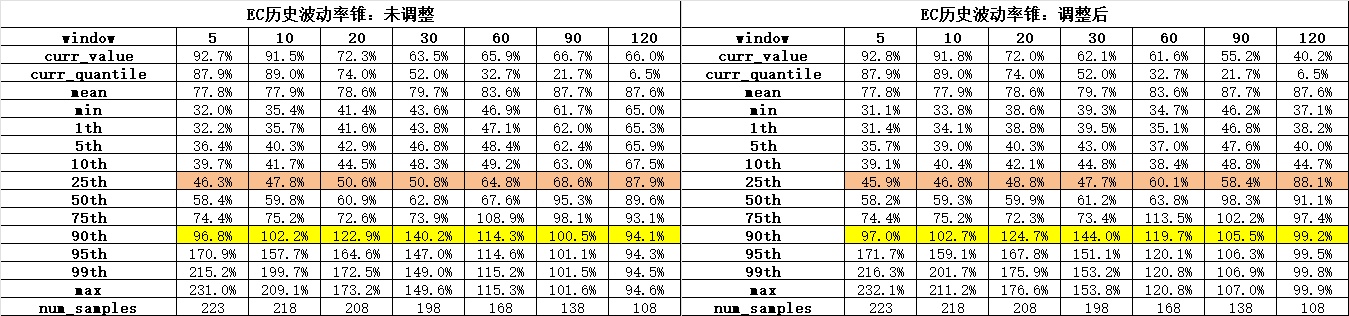
再看另一高波品种纯碱。我们发现纯碱由于样本量充足，在各个窗口下调整对HV的影响均不大。